Hodgkin Huxley Model

I had such a poor understanding of some of the background needed for neurodynamics such as electricity, circuits (hey I'm a software person), biochemistry, and dynamical systems, that I watched several Youtube videos about this model of the neuron before I finally admitted that I needed to read up on the basics of those topics, because I really just didn't understand anything. Here's what I found was missing in my understanding.

Current

"Current" broadly refers to the movement of charged particles and is measured in amps. It tells us how much an electric charge (measured in Coulombs) moves past a certain point in space. I kind of liken it to water flowing in a stream, where if you have a very deep stream you will have more water flowing, and thus more current. In the context of neurons these currents can be injected current, synaptic current, or ionic current. Ionic current refers to ions passing into and out of the neuron through channels in the cell membrane.

Voltage

I didn't know this before, but "voltage" and "volts" refer to different things. "Volts" are a unit of electric potential, which basically means the amount of work (measured in Joules, or (kg * m^2) / s^2) ) it takes to move a charged particle from where it is to some arbitrary point in space. So electric potential is actually a property of space, and one point of space will have a different electric potential than another based on the charges around it. "Voltage" refers specifically to the difference in electrical potential between two points in space. 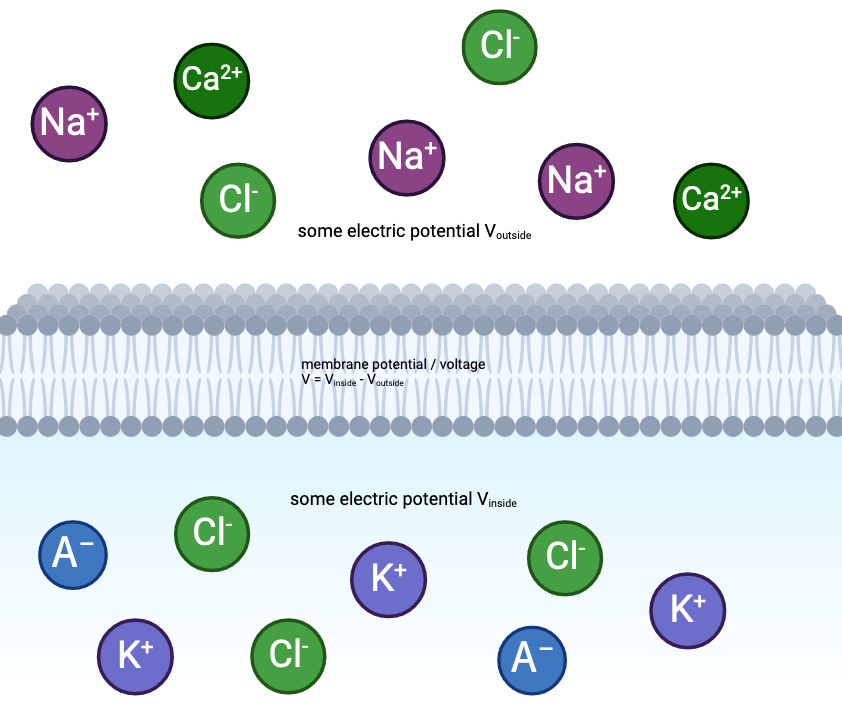So in the context of neurons, you can have an electric potential on one side of the cell membrane, and a different electric potential on the other side, and the voltage is the difference between these potentials. It is also called the membrane potential. I personally find this a little confusing because this thing we call the "membrane potential" is itself a difference between two potentials, but that's the nomenclature.

Resistance / Conductance

Resistance is a measure of how much a material opposes the flow of electric current. For example, you might have a copper-nickel wire and that would have a lower resistance than a nickel-chrome-iron wire simply due to the material.

In the context of neurons, resistance's inverse term conductance is used more frequently. Specific ion channels will have conductances which basically represent how easily ions can pass through them.

Understanding Current and Voltage Relationship

Let's see how current and voltage relate to each other in a simple circuit. This interactive demo lets you experiment with different voltages and resistances to see how they affect current flow:

This relationship is described by Ohm's Law (V = IR), which tells us that:

• Increasing voltage while keeping resistance constant will increase current
• Increasing resistance while keeping voltage constant will decrease current

Capacitance

Another thing I had to wrap my head around was capacitance. Think of it like a rubber balloon - it can stretch to store stuff temporarily. In the case of the cell membrane, it's storing charge separation - having different amounts of charged particles (ions) on either side. This matters because:

1. The cell membrane is made of fatty molecules that repel water (called phospholipids). This creates a barrier that ions can't easily cross.
2. When ions build up on either side of this barrier, it creates an electrical difference (like a tiny battery).
3. The membrane's capacitance affects how quickly the neuron's voltage can change - just like a bigger balloon takes longer to fill.

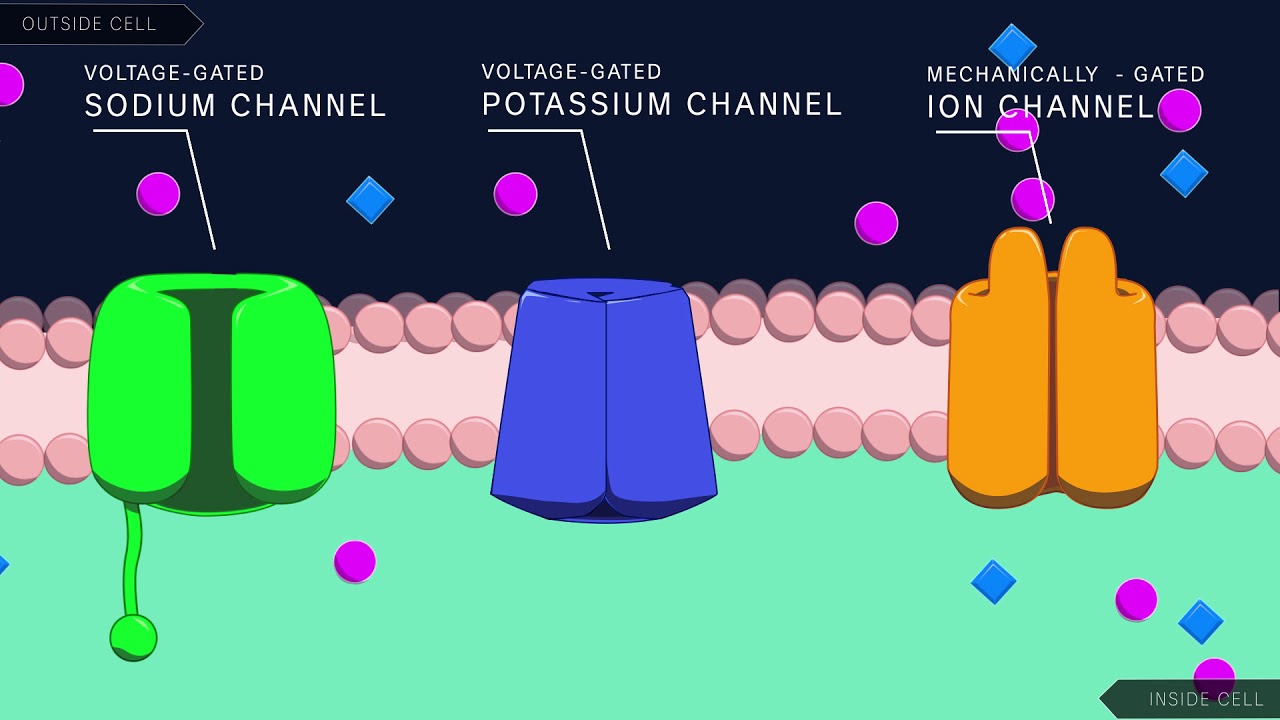
Ion Channels: The Gatekeepers

Looking at that first image above with the green, blue, and orange channels - those are protein structures embedded in the membrane that act like selective gates. They come in different flavors:

1. Voltage-gated channels (the green sodium and blue potassium ones): These open and close based on the voltage across the membrane. It's like having a door that automatically opens when enough pressure builds up on one side.

2. Mechanically-gated channels (the orange ones): These open when they're physically nudged or stretched. Think of them like those push-to-open doors at supermarkets.

The Players: Different Types of Ions

In the second image, we can see the main ions involved in this neural dance:

• Sodium (Na⁺): Mostly hanging out outside the cell
• Potassium (K⁺): Concentrated inside the cell
• Chloride (Cl⁻): Mainly outside
• Large negative molecules (A⁻): Stuck inside

This uneven distribution is super important - it's like setting up a bunch of springs that want to snap back to a relaxed position. When channels open, ions rush through them following both:

1. Their concentration gradient (moving from where there's more to where there's less)
2. Their electrical gradient (positive charges attracted to negative areas and vice versa)

Putting It All Together: The Model

Now, imagine our neuron's membrane as a circuit. Each component represents a real biological feature:

1. The Membrane as a Capacitor
   The membrane itself acts like a capacitor because it can store charge separation. When current flows through a capacitor, it changes the voltage according to:

   $I_c = C_m\frac{dV_m}{dt}$

   where $I_c$ is the capacitive current, $C_m$ is the membrane capacitance, and $\frac{dV_m}{dt}$ is how fast the voltage is changing.

2. Ion Channels as Variable Resistors
   Each type of ion channel can be thought of as a variable resistor (or its inverse, a variable conductor). The current through any ion channel follows a simple rule:

   $I_{ion} = g_{ion}(V_m - V_{ion})$

   where:

   • $g_{ion}$ is the conductance (how easily ions can flow)
   • $V_m$ is the membrane voltage
   • $V_{ion}$ is the equilibrium voltage for that ion (the voltage at which there's no net flow)

3. Channel Types and Their Behaviors

   • Leak Channels: These are always open, with a constant conductance. Think of them as simple holes that always let a small amount of ions through.

   • Voltage-gated Sodium Channels: These are more complex. They have two types of gates:

     • Activation gates ('m'): Open quickly when voltage increases
     • Inactivation gates ('h'): Close slowly when voltage increases The combined conductance looks like: $g_{Na} = \bar{g}_{Na}m^3h$ where $\bar{g}_{Na}$ is the maximum possible conductance

   • Voltage-gated Potassium Channels: These have just activation gates ('n'): $g_K = \bar{g}_Kn^4$

4. Putting the Currents Together
   The total current across the membrane is the sum of all these individual currents:

   $I = C_m\frac{dV_m}{dt} + \bar{g}_Kn^4(V_m - V_K) + \bar{g}_{Na}m^3h(V_m - V_{Na}) + g_L(V_m - V_L)$

   where $g_L$ and $V_L$ represent the leak conductance and voltage.

5. The Gating Variables
   The variables m, h, and n (which control channel opening and closing) each follow their own dynamics:

   $\frac{dx}{dt} = \alpha_x(1-x) - \beta_xx$

   where x could be m, h, or n, and $\alpha$ and $\beta$ are rate constants that depend on voltage.

Think of this system like a complex dance:

1. When voltage starts to increase, sodium channels begin to open (m increases)
2. This lets more sodium in, further increasing voltage
3. But then the sodium channels start to inactivate (h decreases)
4. Meanwhile, potassium channels slowly open (n increases)
5. This combination brings the voltage back down
6. The cycle can then repeat

The genius of Hodgkin and Huxley was figuring out not just these equations, but the actual values of all the parameters. They did this using a clever series of experiments on the giant axon of a squid (which is why we have a squid in our cover image!). They systematically blocked different ion channels and measured the resulting currents, building up piece by piece an understanding of how each component contributed to the whole.

What Happens When We Run This Model?

With the right parameters, this model reproduces the characteristic behavior of neurons - the action potential. When enough current is injected:

1. A rapid upstroke occurs (sodium rushing in)
2. A peak around +40 mV
3. A rapid downstroke (sodium channels inactivating, potassium channels opening)
4. A period where it's harder to generate another spike (the refractory period)

What's amazing is that this relatively simple set of equations captures such complex behavior. It shows how a bunch of ion channels, each following fairly simple rules, can work together to create the binary signaling system that our brains use to process information.

Why This Matters

For someone coming from software (like me), this model is fascinating because it:

1. Shows how a bunch of simple rules about ions and channels can create complex behavior
2. Turns an analog system (continuous voltages) into a digital one (all-or-nothing action potentials)
3. Helps us understand how neurons compute information

In fact, some of the mathematics here (especially the gating variables for ion channels) reminds me of the gates in neural networks, even though they work quite differently. It's a beautiful example of how nature implements computation with some remarkably simple building blocks.